Contemporized IBT Analysis

Jason M. Gleditsch1

06 December 2022

Aim and Scope

Here we run the analyses to determine the relationships between various bank attributes and species richness (SR). First we will create linear models for each species group where bank is the experimental unit, and SR is the response variable. Then we will run models for every combination of explanatory variables and average the models that have 95% of the model weight based on the Akaike Information Criterion corrected for small sample size (AICc). We will then qualitatively compare the averaged model estimates and R squared values for the Exotic, Native, and Total communites for each taxonomic clade using 95% confidence intervals and dot and whisker plots (see ‘Plotting’ vignette for plots).

We then will use the phylogeny to delineate the clades run the analyses again

First we need to load in the caribmacro package.

# required packages
library(caribmacro)

If you do not have this package installed, then run devtools::load_all in order to load all of the necessary functions if you are running this code in the caribmacro R project in the shared folder. If you are not runing this code in the caribmacro R project, then see the functions vignette for the Functions needed.

# Load all of the functions of the caribmacro package
devtools::load_all("./", export_all = FALSE)


## Functions needed ##
#   'sr_LM'  -> returns a list of many SR linear models and their data
#   'AIC_avg'  -> determines the averaged estimates of a dredged global model
#   'r_squared'  -> calculates the r-squared of an averaged model
#   'stndrd'  -> mean centers and divides by sd columns of a data frame
#   'factorize'  -> turns character columns of a data frame into factors

The other R packages needed for this are:

library(here)

# Analysis Packages
library(pwr)
library(MuMIn)
library(qpcR)
library(Hmisc)
library(car)

# Graphing Packages
library(ggplot2)
library(gridExtra)
library(ggpubr)
#library(ggpattern)
library(wesanderson)
library(flextable)

# Phylogenetic Packages
library(ape)
library(phyr)
library(caper)

Now lets load in the species richness data and the bank attributes data.

SR <- read.csv(file.path(here(), 'data_out', 'sr_drivers', 'SR_Drivers_Herp_SR.csv'), header = TRUE)
bank_dat <- read.csv(file.path(here(), 'data_out', 'IBT_Bank_Data.csv'), header = TRUE)
# Make bank in the format of row names
bank_dat$bank<-gsub(".", " ", bank_dat$bank, fixed = TRUE)

# Change NAs in the Lloyd vessel and port counts to 0
bank_dat[is.na(bank_dat$ships), 'ships'] <- 0
bank_dat$pop_dens <- bank_dat$pop_avg/bank_dat$Area

# Invert the Ships Variable
bank_dat$econ_iso <- 1/(bank_dat$ships + 1)

These data can also be found on Dryad at https://doi.org/10.5061/dryad.vx0k6djtn. If you download those data, then skip the Data Checking section and go straight to the Species Richness Analysis section after running the following code.

You can download the files manually or by using the ‘rdryad’ package (https://github.com/ropensci/rdryad).

SR <- read.csv(file.path(here(), 'data_out', 'sr_drivers', 'supp_info', 'dryad', 'Gleditsch_et_al_Caribbean_Herp_SR.csv'), header = TRUE)
bank_dat <- read.csv(file.path(here(), 'data_out', 'sr_drivers', 'supp_info', 'dryad', 'Gleditsch_et_al_Caribbean_Bank_Data.csv'), header = TRUE)

# Transform the SR data into a wide format so that there is a row for each bank 
SR[which(SR$Clade == 'All Herpetofauna'), 'Clade'] <- 'All'
clds <- levels(as.factor(SR$Clade))
out <- SR[which(SR$Clade == 'All'), c("Bank", "Introduced_SR", "Native_SR", "Total_SR")]
names(out) <- c('bank', paste('All', c('E', 'N', 'T'), sep = '.'))
for (i in 2:length(clds)) {
  tmp <- SR[which(SR$Clade == clds[i]), c("Bank", "Introduced_SR", "Native_SR", "Total_SR")]
  names(tmp) <- c('bank', paste(clds[i], c('E', 'N', 'T'), sep = '.'))
  out <- merge(out, tmp, by = 'bank', all = TRUE)
  if (nrow(out) != nrow(tmp)) {
    stop('Error in merge; NAs produced')
  }
  rm(tmp)
}
SR <- out
rm(out)


# Change the names of the columns in the bank data to match what is used in the analysis
## -> bank = Bank
## -> Number = Number_of_Islands
## -> Area = Geographic_Area
## -> source = Geographic_Isolation
## -> Spread = Island_Spread
## -> econ_iso = Economic_Isolation
## -> pop_avg = Average_Population
## -> DEM.sd = Topographic_Complexity
## -> anthro = Anthropogenic_Habitat
## -> green = Green_Habitat
names(bank_dat) <- c("bank", "Number", "Area", "source", "Spread", "econ_iso", "pop_avg", "DEM.sd", "anthro", "green")

Data Checking

Check for multicollinearity

We will start by checking to see if the bank attribute data is correlated so that we can select appropriate explanatory variables for the models. However, we already know some of the variables we want in the models so let’s just check for multicollinearity in those right now.

# Select bank variables
vars <- c('Area', 'min', 'source', 'Number', 'Spread', 'DEM.sd',
          'green', 'anthro', 'pop_dens', 'ships', 'econ_iso')

#Check for highly correlated bank variables
tmp <- bank_dat[, vars]
tmp$Area <- log(tmp$Area)
tmp <- stndrd(vars, tmp)

cors <- cor(tmp, use = "pairwise.complete.obs")

cor.chk <- data.frame(NULL)

for (i in 1:ncol(cors)) {
  v2 <- names(cors[which(abs(cors[, i]) >= 0.5), i])
  v2 <- v2[which(v2 != colnames(cors)[i])]
  rs <- cors[v2, i]
  names(rs) <- NULL
  tmp <- data.frame(Var.1 = rep(colnames(cors)[i], length(v2)),
                    Var.2 = v2,
                    r = rs)

  cor.chk <- rbind(cor.chk, tmp)
  rm(v2, rs, tmp)
}


bad <- cor.chk[which(abs(cor.chk$r) >= 0.5 & cor.chk$Var.1 != 'ships' & cor.chk$Var.2 != 'ships'), ]
tab <- flextable(bad[!duplicated(bad[, 'r']),])
tab <- bg(tab, bg = 'grey90', part = 'all')
theme_vanilla(tab)

As we can see Area is correlated with topographical complexity and the economic isolation (Pearson r = and ). In addition topographical complexity and the economic isolation are correlated with each other (Person r = ).

Select Explanatory Variables

Even though Area, topographical complexity (‘DEM.sd’), and the number of ship visits (‘ships’) are all correlated with each other, they are thought to be important for our understanding of island biogeography so we will retain these variables. In addition, the variation inflation factor for these variables were not above 3 suggesting that they do not create issues of multicolinearity in the model. Still, any interpretations of these coefficients should be done with caution.

mod <- lm(SR ~ Area + Spread + source + DEM.sd + green + anthro + pop_dens + econ_iso, data = dat)
tmp <- round(data.frame(VIF = vif(mod)), 4)
tmp$Variable <- row.names(tmp)

tab <- flextable(tmp[, c('Variable', 'VIF')])
tab <- bg(tab, bg = 'grey90', part = 'all')
theme_vanilla(tab)

We will remove the distance to the nearest bank (‘min’) and number of islands (‘Number’). This is based off of initial analyses showing the lack of importance of these variables in explaining the SR patterns. We will also remove the non-inverted number of ship visits (‘ships’).

vars <- vars[which(vars != 'Number' & vars != 'min' & vars != 'ships')]
#vars <- vars[which(vars != 'min')]

# Save the explanatory variables for the node analysis just in case
nod.v <- vars

Species Richness Analysis

Clade Select

It is important that we only retain the species groups that are found on enough island banks to have enough statistical power to determine the relationship. The data found on Dryad have already been reduced to the clades with enough statistical power, and therefore, if using that data, skip to the Create SR Models section.

To determine the ideal number of banks needed to have a power of 0.8, we will use the pwr.f2.test function in the ‘pwr’ package. For this, we will need to estimate the R2 of the SARs. We will use the SAR for all of the reptile and amphibian species to estimate the desired R2.

# Manipulate data
dat <- merge(SR[, c('bank', 'All.T')], bank_dat, by = 'bank', all = TRUE)
dat <- dat[complete.cases(dat[, vars]), ]
dat <- dat[!is.na(dat$All.T), ]

dat$Area <- log(dat$Area)
dat$All.T <- log(dat$All.T + 1)

dat <- stndrd(vars = c('All.T', vars), data = dat)

# Determine the needed number of banks (n)
# We will set the number of estimates to 9 
m.all <- lm(All.T ~ Area + source + Spread + DEM.sd + green + anthro + pop_dens + econ_iso, 
            data = dat)
all.avg <- AIC_avg(m.all,
                   data = dat,
                   response = 'All.T',
                   x_vars = vars,
                   groups = data.frame(Genus = 'All',
                                       Status = 'T'),
                   cum.weight = 0.95,
                   table = FALSE,
                   std = 'partial.sd')

tmp.v <- attr(m.all$terms,'term.labels')
R2 <- r_squared(all.avg[, c('Variable', 'Estimate')],
                data = dat,
                response = 'All.T',
                x_vars = tmp.v,
                display = FALSE)[1, 1]

n <- round(1 + pwr.f2.test(u = 8, f2 = R2/(1 - R2), power = 0.8)[['u']] + 
               pwr.f2.test(u = 8, f2 = R2/(1 - R2), power = 0.8)[['v']], 0)

# Select the clades that have at least 1 sp on >/= n banks
tmp <- SR
for (i in 2:ncol(tmp)) {
  tmp[which(tmp[, i] < 1), i] <- 0
  tmp[which(tmp[, i] >= 1), i] <- 1
}

good <- names(colSums(tmp[, names(tmp)[grep(".T", names(tmp), fixed = TRUE)]])[
  which(colSums(tmp[, names(tmp)[grep(".T", names(tmp), fixed = TRUE)]]) >= n)])
good <- sub('.T', '.', good)

out <- data.frame(bank = SR$bank)

for (i in 1:length(good)) {
  if (sum(tmp[, names(tmp)[grep(good[i], names(tmp), fixed = TRUE)]][, 1]) >= n &
      sum(tmp[, names(tmp)[grep(good[i], names(tmp), fixed = TRUE)]][, 2]) >= n &
      sum(tmp[, names(tmp)[grep(good[i], names(tmp), fixed = TRUE)]][, 3]) >= n) {
    out <- merge(out, SR[, c('bank', names(SR)[grep(good[i], names(SR), fixed = TRUE)])], 
                 by = 'bank', all = TRUE)
  } else {NA}
}


tmp <- unique(substr(setdiff(names(SR), names(out)), 1, nchar(setdiff(names(SR), names(out)))-2))

# To print the names of the clades removed
cat(paste0('Groups with not enough banks (n = ', length(tmp), ')', '\n', '\n',
          paste(tmp, collapse = " | ")))
## Groups with not enough banks (n = 180)
## 
## Agalychnis | Alinea | Alligatoridae | Allobates | Alsophis | Ameiva | Amerotyphlops | Amphisbaena | Amphisbaenia | Anguimorpha | Aristelliger | Aromobatidae | Arrhyton | Aspidoscelis | Atractus | Bachia | Basiliscus | Boa | Boana | Boidae | Borikenophis | Bothrops | Bufonidae | Cadea | Caiman | Capitellum | Caraiba | Celestus | Centrochelys | Chelidae | Chelonoidis | Chelus | Chilabothrus | Chironius | Clelia | Cnemidophorus | Coleonyx | Coluber | Colubridae | Coniophanes | Copeoglossum | Corallus | Corytophanes | Corytophanidae | Cricosaura | Crocodylus | Crotalus | Ctenosaura | Cubophis | Cyclura | Dendropsophus | Diploglossidae | Diploglossus | Dipsadidae | Dipsas | Drymarchon | Drymobius | Dryophytes | Elachistocleis | Emydidae | Engystomops | Enulius | Epicrates | Epictia | Erythrolamprus | Eunectes | Eusuchia | Flectonotus | Gastrophryne | Gekko | Gekkonidae | Gonatodes | Gymnophthalmidae | Gymnophthalmus | Haitiophis | Helicops | Hemidactylus | Holcosus | Hyalinobatrachium | Hydrops | Hyla | Hypsiboas | Hypsirhynchus | Ialtris | Iguana | Imantodes | Incilius | Indotyphlops | Kentropyx | Kinosternon | Lachesis | Leiocephalus | Leiuperidae | Lepidodactylus | Leptodactylus | Leptodeira | Leptophis | Leptotyphlopidae | Liotyphlops | Lithobates | Mabuya | Magliophis | Malaclemys | Mannophryne | Marisora | Mastigodryas | Mesoclemmys | Mesoscincus | Microhylidae | Micrurus | Mitophis | Nerodia | Ninia | Opheodrys | Oreosaurus | Osteopilus | Oxybelis | Oxyrhopus | Paleosuchus | Pantherophis | Pelophylax | Peltophryne | Pelusios | Pholidoscelis | Phrynonax | Phyllodactylidae | Phyllodactylus | Phyllomedusa | Phytotriades | Pipa | Plestiodon | Pleurodema | Pleurodira | Plica | Polychrus | Pristimantis | Pseudelaphe | Pseudemys | Pseudis | Pseudoboa | Ranidae | Rhinella | Rhinoclemmys | Scarthyla | Sceloporus | Scinax | Scincella | Scincidae | Scincomorpha | Sibon | Siphlophis | Smilisca | Sphaenorhynchus | Sphaerodactylidae | Sphaerodactylus | Spilotes | Spondylurus | Storeria | Tantilla | Tantillita | Tarentola | Teiidae | Testudinidae | Tetracheilostoma | Thamnodynastes | Thamnophis | Thecadactylus | Tlalocohyla | Trachemys | Trachycephalus | Tretanorhinus | Tretioscincus | Tropidophis | Tropiduridae | Tropidurus | Tupinambis | Typhlops | Uromacer | Varzea | Viperidae
cat(paste0('\n\n R^2 of complete model = ', R2, '\n\n'))
## 
## 
##  R^2 of complete model = 0.711540544458035
cat(paste0('Minimum number of banks present = ', n, '\n\n'))
## Minimum number of banks present = 16
SR <- out
rm(tmp, out, m.all, tmp.v, all.avg)

Remove Other Unwanted Clades

Because we do not want the banks with no species of a certain clade in our analyses, let’s turn the instances when the total species richness of a clade is 0 to NA as well as the corresponding native and exotic SR values. In other words, all instances when exotic, native, and total SR are equal to zero will be changed to NA, effectively removing them from the analyses.

groups <- names(SR)[grep(".T", names(SR), fixed = TRUE)]
groups <- sub('.T', '.', groups)

for (i in 1:length(groups)) {
  SR[which(SR[, paste(groups[i], 'T', sep = '')] == 0),
     names(SR)[grep(groups[i], names(SR), fixed = TRUE)]] <- NA
}

Additionally, we do not want to include clades that are the same as other clades (i.e. have the same species as another clade). To do this we need the taxonomy for each species so that we can check clade species lists to each other.

taxa <- read.csv(file.path(here(), 'data_out', 'supp_info', 'IBT_Carib_Taxonomy.csv'), header = TRUE)
taxa[which(taxa$Family=='Natricidae'), 'Family'] <- 'Colubridae'

groups <- names(SR)[grep(".T", names(SR), fixed = TRUE)]
groups <- sub('.T', '', groups)

tmp.lists <- NULL
for(i in 1:length(groups)) {
  if (is.element(groups[i], taxa$Class)) {
    tmp <- taxa[which(taxa$Class == groups[i]), c('Class', 'binomial')]
  } else if (is.element(groups[i], taxa$Order)) {
    tmp <- taxa[which(taxa$Order == groups[i]), c('Order', 'binomial')]
  } else if (is.element(groups[i], taxa$Suborder)) {
    tmp <- taxa[which(taxa$Suborder == groups[i]), c('Suborder', 'binomial')]
  } else if (is.element(groups[i], taxa$Family)) {
    tmp <- taxa[which(taxa$Family == groups[i]), c('Family', 'binomial')]
  } else if (is.element(groups[i], taxa$Genus)) {
    tmp <- taxa[which(taxa$Genus == groups[i]), c('Genus', 'binomial')]
  } else {
    tmp <- data.frame(Clade = groups[i], Species = NA)
  }
  
  names(tmp) <- c('Clade', 'Species')
  tmp.lists <- rbind(tmp.lists, tmp)
}
sp.lists <- tmp.lists[!is.na(tmp.lists$Species), ]

# Clades not found in Taxonomy file
tmp.lists[is.na(tmp.lists$Species), ]
##   Clade Species
## 1   All    <NA>
groups <- groups[!is.element(groups, tmp.lists[is.na(tmp.lists$Species), 'Clade'])]

chk <- NULL
for(i in 1:length(groups)) {
  tmp.g <- groups[which(groups != groups[i])]
  
  for (j in 1:length(tmp.g)) {
    tmp.1 <- sp.lists[which(sp.lists$Clade == groups[i]), ]
    tmp.2 <- sp.lists[which(sp.lists$Clade == tmp.g[j]), ]
    if (length(tmp.1$Species) == length(tmp.2$Species)) {
      if (!is.na(all(match(tmp.1$Species, tmp.2$Species)))) {
        chk <- rbind(chk, data.frame(Clade.1 = groups[i], Clade.2 = tmp.g[j], chk = TRUE))
      } else {
        chk <- rbind(chk, data.frame(Clade.1 = groups[i], Clade.2 = tmp.g[j], chk = FALSE))
      }
    } else {
      chk <- rbind(chk, data.frame(Clade.1 = groups[i], Clade.2 = tmp.g[j], chk = FALSE))
    }
  }
}

chk[chk$chk, ]
## [1] Clade.1 Clade.2 chk    
## <0 rows> (or 0-length row.names)

We are also going to remove the Anura clade. This is because the Anura clade has one more species than the Neobatrachia clade and one less species than the Amphibia clade.

SR <- SR[, names(SR)[which(names(SR) != 'Anura.T' & names(SR) != 'Anura.E' & names(SR) != 'Anura.N')]]
cat('Number of clades = ', (ncol(SR)-1)/3, '\n', '\n', 'R^2 = ', R2, '\n', '\n')
## Number of clades =  16 
##  
##  R^2 =  0.7115405 
##

Create SR Models

Now that we removed the zeros, lets create the SR models. To do this we will use the sr_LM() function of the ‘caribmacro’ package. This function creates a list of ordinary linear models, with species richness as the response variable, that can be used in later analyses. Since we will use these models in AIC Model Averaging, it is important to only use data with complete cases so therefore we will set complete.case = TRUE. Additionally, this argument causes the function to return a list of length 2 with the first element (named ‘Models’) holding a list of j models where j is equal to the number of species groups. The second element (named ‘Data’) of that list is a list of j data frames that were used to create those models.

system.time(lm.sr <- sr_LM(SR = SR,
                           data = bank_dat,
                           x_vars = vars,
                           geo_group = 'bank',
                           area = 'Area',
                           standardize = TRUE,
                           log_area = TRUE,
                           sq_area = FALSE,
                           complete.case = TRUE))
##    user  system elapsed 
##    0.04    0.00    0.05

SR AIC Model Averaging

Now that we have created a list of models, we can use them as global models in AIC Model Averaging. For each model, a set of models with every combination (including the intercept only) of explanatory variables is created. Those models are then ranked based on there AICc and their Akaike weights (i.e. the relative likelihood of the model) determined. We then select the models that have 95% of the cumalative model weight and using the weights calculate the weighted average of the model estimates. All of these steps have been incorporated in the AIC_avg() function of the ‘caribmacro’ package.

Because some of our explanatory variables are slightly correlated we will weight the estimates of each model to be averaged based on the partial standard deviation (see Cade 2015). This can be done in the AIC_avg() function with the ‘std’ argument.

mods <- lm.sr[['Models']]
data <- lm.sr[['Data']]

nams<-strsplit(names(mods), ".", fixed = TRUE)
nams<-data.frame(matrix(unlist(nams), nrow = length(nams), byrow = TRUE))
names(nams) <- c('Taxon', 'Group')
nams$Taxon <- as.character(nams$Taxon)
nams$Group <- as.character(nams$Group)

Avg.SR <- data.frame(NULL)
AIC_Tabs <- vector('list', length(mods))
names(AIC_Tabs) <- names(mods)
pb <- winProgressBar(title = "Progress Bar", min = 0, max = length(mods), width = 300)
system.time(for (i in 1:length(mods)) {
  dat <- data[[i]]
  out <- suppressMessages(AIC_avg(mods[[i]],
                                  data = dat,
                                  response = names(mods)[i],
                                  x_vars = vars,
                                  groups = nams[i, ],
                                  cum.weight = 0.95,
                                  table = TRUE,
                                  std = 'partial.sd'))
  Avg.SR <- rbind(Avg.SR, out[['Coefficients']])
  AIC_Tabs[[names(mods[i])]] <- out[['AIC Table']]

  rm(dat, out)
  setWinProgressBar(pb, i, title=paste( round(i/length(mods)*100, 0), "% Done", sep = ''))
  if (i == length(mods)) {
    close(pb)
    cat('DONE! \n')
  } else {NA}
})
## DONE!
##    user  system elapsed 
##   37.36    0.77   38.31

Now let’s export the results to the ‘data_out’ folder.

write.csv(Avg.SR, file.path(here(), 'data_out', 'results', 'sr_drivers', 'SR_Drivers_std_Estimates.csv'),
          row.names=FALSE)

To further determine how the importance of island metrics change between the different assemblages, we will look at the representation of the metrics in the models that make up 95% of the cumulative model weight.

aic.p <- NULL
for (i in 1:length(AIC_Tabs)) {
  
  # Determine the cumulative weight and select top models
  AIC_Tabs[[i]]$cum.wt <- NA
  
  for (j in 1:nrow(AIC_Tabs[[i]])) {
    AIC_Tabs[[i]][j, 'cum.wt'] <- sum(AIC_Tabs[[i]]$weight[1:j])
  }
  
  tmp <- AIC_Tabs[[i]][which(AIC_Tabs[[i]]$cum.wt <= 0.95), ]
  
    # Determine the proportion of the top models that have each variable
  out3 <- data.frame(Model = names(AIC_Tabs[i]),
                     Area = nrow(tmp[!is.na(tmp$Area), ])/nrow(tmp),
                     Spread = nrow(tmp[!is.na(tmp$Spread), ])/nrow(tmp),
                     DEM.sd = nrow(tmp[!is.na(tmp$DEM.sd), ])/nrow(tmp),
                     green = nrow(tmp[!is.na(tmp$green), ])/nrow(tmp),
                     anthro = nrow(tmp[!is.na(tmp$anthro), ])/nrow(tmp),
                     source = nrow(tmp[!is.na(tmp$source), ])/nrow(tmp),
                     econ_iso = nrow(tmp[!is.na(tmp$econ_iso), ])/nrow(tmp),
                     pop_dens = nrow(tmp[!is.na(tmp$pop_dens), ])/nrow(tmp))
  aic.p <- rbind(aic.p, out3)

  rm(tmp, out3)
}

aic.p$Clade <- data.frame(matrix(unlist(strsplit(aic.p$Model, '.', fixed = TRUE)), 
                                 nrow = length(strsplit(aic.p$Model, '.', fixed = TRUE)), 
                                 byrow = TRUE))$X1
aic.p$Group <- data.frame(matrix(unlist(strsplit(aic.p$Model, '.', fixed = TRUE)), 
                                 nrow = length(strsplit(aic.p$Model, '.', fixed = TRUE)), 
                                 byrow = TRUE))$X2
aic.p$Assemblage <- NA
aic.p[which(aic.p$Group == 'N'), 'Assemblage'] <- 'Native'
aic.p[which(aic.p$Group == 'E'), 'Assemblage'] <- 'Introduced'
aic.p[which(aic.p$Group == 'T'), 'Assemblage'] <- 'Total'
write.csv(aic.p, file.path(here(), 'data_out', 'results', 'sr_drivers', 'supp_info', 'SR_Drivers_aic_prop.csv'),
          row.names=FALSE)

Explore the SR results

Let’s explore some of the results of the SR analyses.

We will first look at the general trends and the relationships for the major clades (all herps, reptilia, and amphibia). To look athe the general trends we will calculate the mean coefficient across all clades (except the all herp clade) weighted by the effect size (Cohen’s f2) of the clade’s average model.

Cohen’s f2 is based on the model fit (R2) which we calculated in the background (see the Model Fit section below for the code used to determine the R2 for the models). We also calculate the weighted standard errors and coefficients of variation (CV) for each relationship to investigate the variablility of the relationships across clades.

grp <- levels(as.factor(Avg.SR$Group))

R.sq_sr$f2 <- R.sq_sr$R.sq/(1 - R.sq_sr$R.sq)
temp <- merge(Avg.SR, R.sq_sr[, c("Taxon", "Group", "R.sq", "f2")], by = c("Taxon", "Group"), all = TRUE)

w.avg.est2 <- NULL
for (i in 1:length(vars)) {
  tmp1 <- droplevels(temp[which(temp$Variable == vars[i] & temp$Taxon != 'All'), ])
  
  for (j in 1:length(grp)) {
    tmp2 <- data.frame(Variable = vars[i], Group = grp[j],
                       Sample.Size = nrow(tmp1[which(tmp1$Group == grp[j]), ]),
                       Estimate = wtd.mean(tmp1[which(tmp1$Group == grp[j]), 'Estimate'], 
                                           tmp1[which(tmp1$Group == grp[j]), 'f2']),
                       Variance = wtd.var(tmp1[which(tmp1$Group == grp[j]), 'Estimate'],
                                          tmp1[which(tmp1$Group == grp[j]), 'f2'], method = 'unbiased'))
    w.avg.est2 <- rbind(w.avg.est2, tmp2)
    rm(tmp2)
  }
  
  rm(tmp1)
}
w.avg.est2$SD <- sqrt(w.avg.est2$Variance)
w.avg.est2$SE <- w.avg.est2$SD/sqrt(w.avg.est2$Sample.Size)
w.avg.est2$CV <- w.avg.est2$SD/abs(w.avg.est2$Estimate)
write.csv(w.avg.est2, file.path(here(), 'data_out', 'results', 'sr_drivers', 'SR_Drivers_weighted_avg_estimates.csv'),
          row.names=FALSE)
## Warning: Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.
## ℹ Please use `linewidth` instead.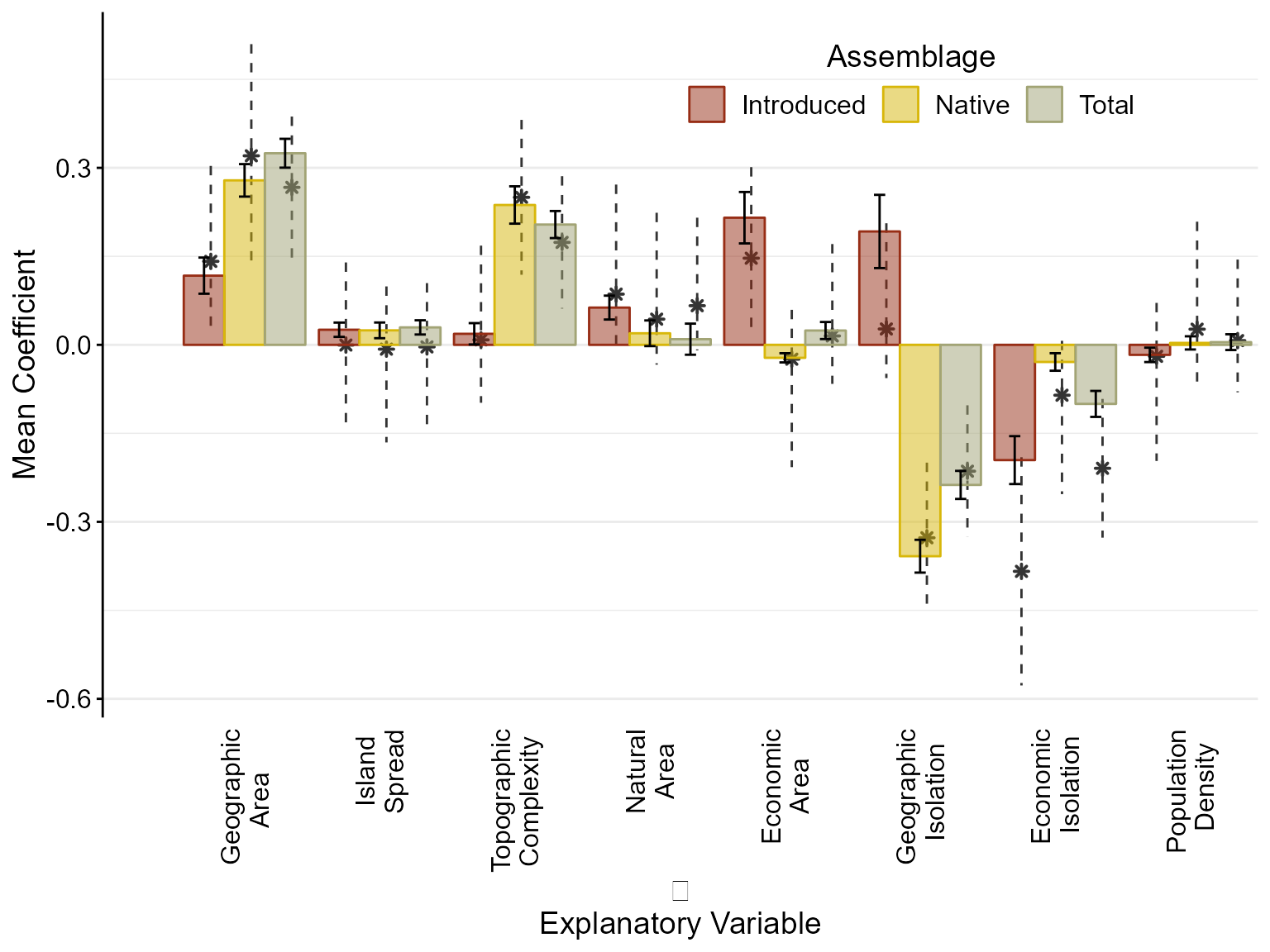

We see that across all of the herpetofaunal clades, area and isolation had the largest effects on species richness. Larger banks, in terms of land area, overall had more native and introduced species richness, and therefore, area had a greater effect on total species richness patterns. Conversely, banks that were further from an evolutionary source had less native and more introduced species, resulting in a decreased effect of isolation on total species richness patterns.

Additionally, the more topographical complexity on a bank increased native species richness but had little effect on introduced species richness. This caused the effect on total species richness to be slightly reduced. On the other hand, more anthropogenic habitat increased introduced species richness causing anthropogenic habitat to a larger effect on total species richness. Similarly, more ship visits to a bank increased introduced species richness causing ship visits to have more of an effect on total species richness.

The amount of green habitat on a bank had overall small positive effects on species richness, but increased introduced species richness more than native and total species richness. Island spread had small positive effects that were similar between the three species assemblages (i.e. native, introduced, and total) and population density did not have consistent effects overall.

## TableGrob (3 x 3) "arrange": 9 grobs
##        z     cells    name           grob
## area   1 (1-1,1-1) arrange gtable[layout]
## spread 2 (1-1,2-2) arrange gtable[layout]
## topo   3 (1-1,3-3) arrange gtable[layout]
## green  4 (2-2,1-1) arrange gtable[layout]
## anthro 5 (2-2,2-2) arrange gtable[layout]
## iso    6 (2-2,3-3) arrange gtable[layout]
## ships  7 (3-3,1-1) arrange gtable[layout]
## pop    8 (3-3,2-2) arrange gtable[layout]
## legend 9 (3-3,3-3) arrange gtable[layout]
# Add clade abbreviation for the figures
cld.abbr <- read.csv(file.path(here(), 'data_out', 'Clade_E_N_SR.csv'), header = TRUE)
cld.abbr <- cld.abbr[, c('Clade', 'Abbreviation', 'Class')]
names(cld.abbr) <- c('Clade', 'Abbr', 'Class')
abbr.ord.gr <- c(1, 2, 13, 10, 5, 14, 16, 15, 18, 6, 8, 7, 9, 11, 12, 3, 17, 4)

aic.p <- merge(aic.p, cld.abbr, by = 'Clade', all = TRUE)
aic.p$Abbr.GR <- factor(aic.p$Abbr, unique(aic.p$Abbr)[abbr.ord.gr])
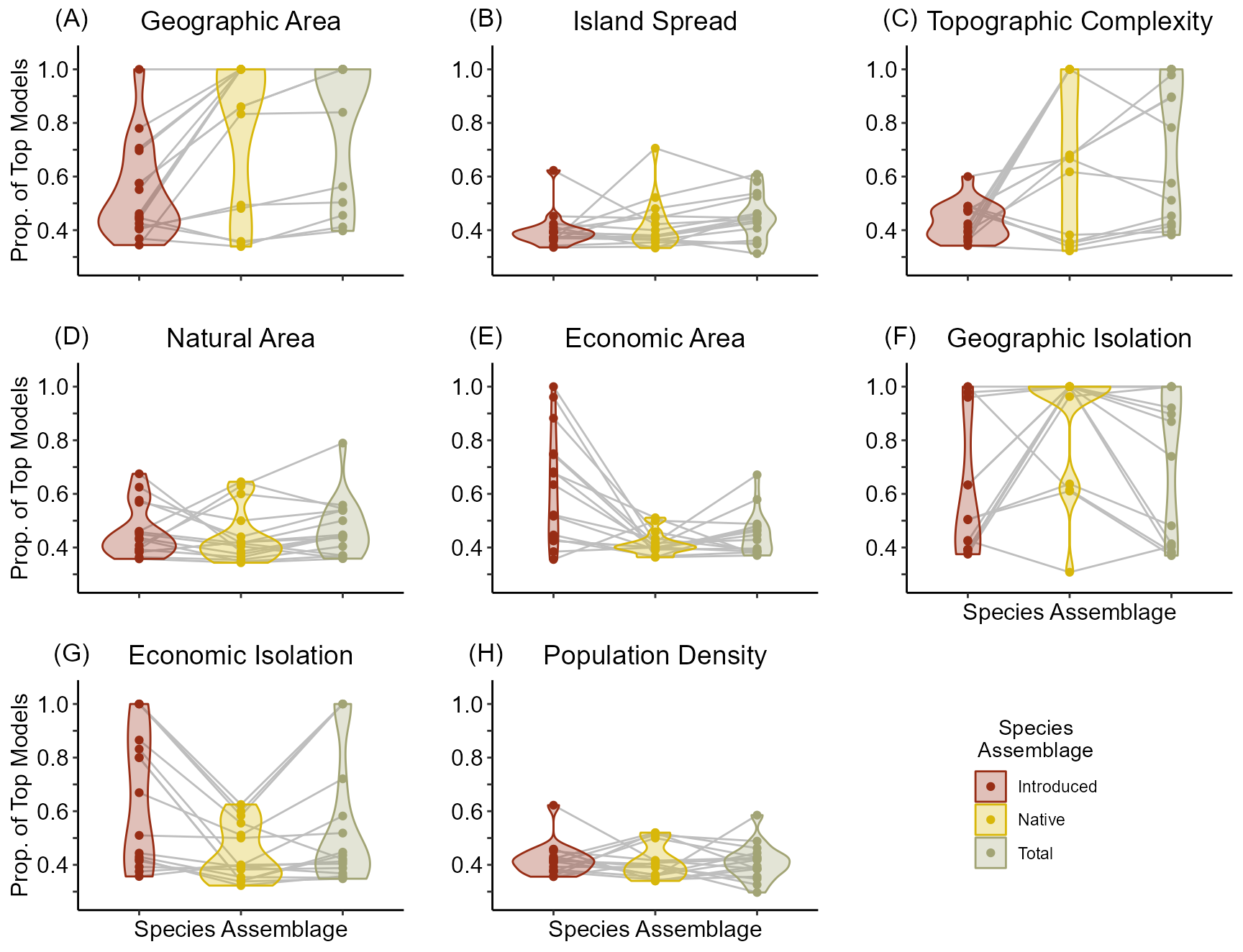
aic.p[which(aic.p$Clade == 'All'), 'Class'] <- 'All'

As is shown in the below figure, the importance of Geographic Isolation is less for many clades in determining the contemporary species richness than native species richness. In addition, Economic Area is important for introduced species but not for native species. Conversely, Topographic complexity and Geographic Area are most important for native and total species richness.

\(\space\)

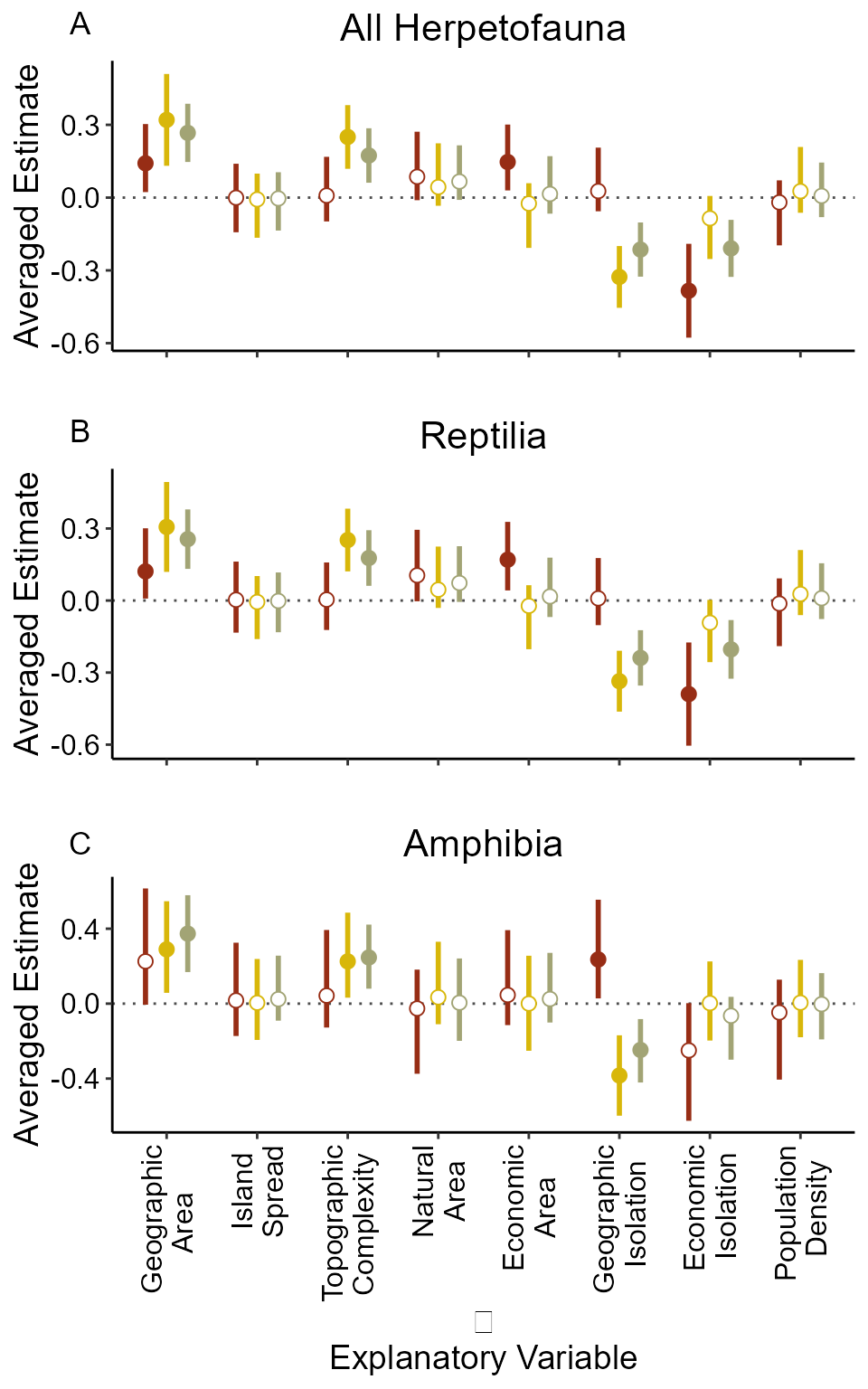
No let’s see how these results vary across the taxonomic groups. First we will look at the model estimates for all Herpetofauna in the Caribbean.

\(\underline{Herpetofauna:}\)

# Native herpetofauna community
tmp <- Avg.SR[which(Avg.SR$Taxon == 'All' & Avg.SR$Group == 'N'), ]
order <- c(1, 3, 9, 4, 5, 2, 8, 6, 7)
tmp$Variable <- factor(tmp$Variable, levels(as.factor(tmp$Variable))[order])
tmp <- tmp[order(tmp$Variable), ]
tmp$Sig <- ' '
tmp[which(tmp$LCL < 0 & tmp$UCL < 0), 'Sig'] <- '*'
tmp[which(tmp$LCL > 0 & tmp$UCL > 0), 'Sig'] <- '*'

tab <- flextable(tmp[, c('Taxon', 'Assemblage', 'Variable', 'Estimate', 'LCL', 'UCL', 'Sig')])
tab <- colformat_double(tab, digits = 3)
tab <- align(tab, align = "center")
tab <- align(tab, j = 1:3, align = "right")
tab <- align(tab, j = 7, align = "left")
tab <- color(tab, i = 1, j = 7, color = "grey90", part = "header")
tab <- bold(tab, i = ~ Sig == '*')
tab <- width(tab, j = 'Sig', width = 0.1)
tab <- bg(tab, bg = 'grey90', part = 'all')
theme_vanilla(tab)

We can see that for Native (Group N) herpetofauna communities there is a stronger curvilinear relationship between SR and Area than there is in the Exotic (Group E) or the Total (Group T) communities. In fact for the Exotic communities the curvilinear relationship has become linear. The other relationships are similar except for the relationship between herpetofauna SR and land cover. For the Native and Total communities, SR is positively related to the percent of green (i.e. natural) land cover. While for the Exotic community, SR is positively related to the percent of anthropogenic land cover.

Now we can see how this compares to other clades starting with the larger clades.

\(\space\)

\(\space\)

\(\underline{Reptilia:}\)

\(\space\)

\(\space\)

\(\underline{Amphibia:}\)

Now let’s look at the clades of lower taxonomic level. We will highlight Anolis and Eleutherodactylus (the most speciose tetrapod genera) by showing their estimates in tables below the figure.

fig.3 <- vector('list', length(vars.fig3))
names(fig.3) <- c('area', 'spread', 'topo', 'green', 'anthro', 'iso', 'ships', 'pop')
for (i in 1:(length(vars.fig3))) {
  temp <- droplevels(Avg.est[which(Avg.est$Variable == vars.fig3[i] & Avg.est$Abbr.GR != 'Herp'), ])
  p <- ggplot(temp, aes(x = Abbr.GR, y = Estimate, color = Assemblage, shape = Class, fill = Fills)) +
          geom_hline(yintercept = 0, linetype = 'dotted', color = 'gray30') +
          geom_errorbar(aes(ymin = LCL, ymax = UCL), position = position_dodge(width = 0.7),
                        width = 0, size = 1) +
          geom_point(size = 2, position = position_dodge(width = 0.7)) +
          scale_color_manual(values = cols) +
          scale_shape_manual(values = c(21, 24)) +
          scale_fill_manual(values = UINT.cols[intersect(names(UINT.cols), unique(temp$Fills))]) +
          scale_y_continuous(labels = scaleFUN) +
          ggtitle(tits.F3[i]) + xlab('Taxonomic Clade') + labs(tag = panels.F3[i]) +
          theme_classic() +
          theme(legend.position = "none", axis.title = element_text(size = 12, color = 'black'),
                axis.text.x = element_text(angle = 90, size = 12, hjust = 1, vjust = 0.5, color = 'black'),
                axis.text.y = element_text(size = 12, color = 'black'),
                plot.title = element_text(hjust = 0.5, size = 14),
                plot.tag.position = c(0.155, 0.975))
  
  if ((i %% 2) == 0) {
    p <- p + theme(axis.title.y = element_text(angle = 90, size = 12, color = 'white'))
  } else {
    p <- p + theme(plot.tag.position = c(0.155, 0.975))
  }
  
  if (is.element(i, c(1:length(vars.fig3)-2))) {
    p <- p + theme(axis.title.x = element_text(size = 12, color = 'white'),
                   axis.text.x = element_blank())
  } else {
    p <- p + theme(axis.title.x = element_text(size = 12, color = 'white'))
  }
  
  fig.3[[i]] <- p
}

\(\space\)

\(\space\)

\(\underline{Natural \space Variables:}\)

## Warning: The `<scale>` argument of `guides()` cannot be `FALSE`. Use "none" instead as
## of ggplot2 3.3.4.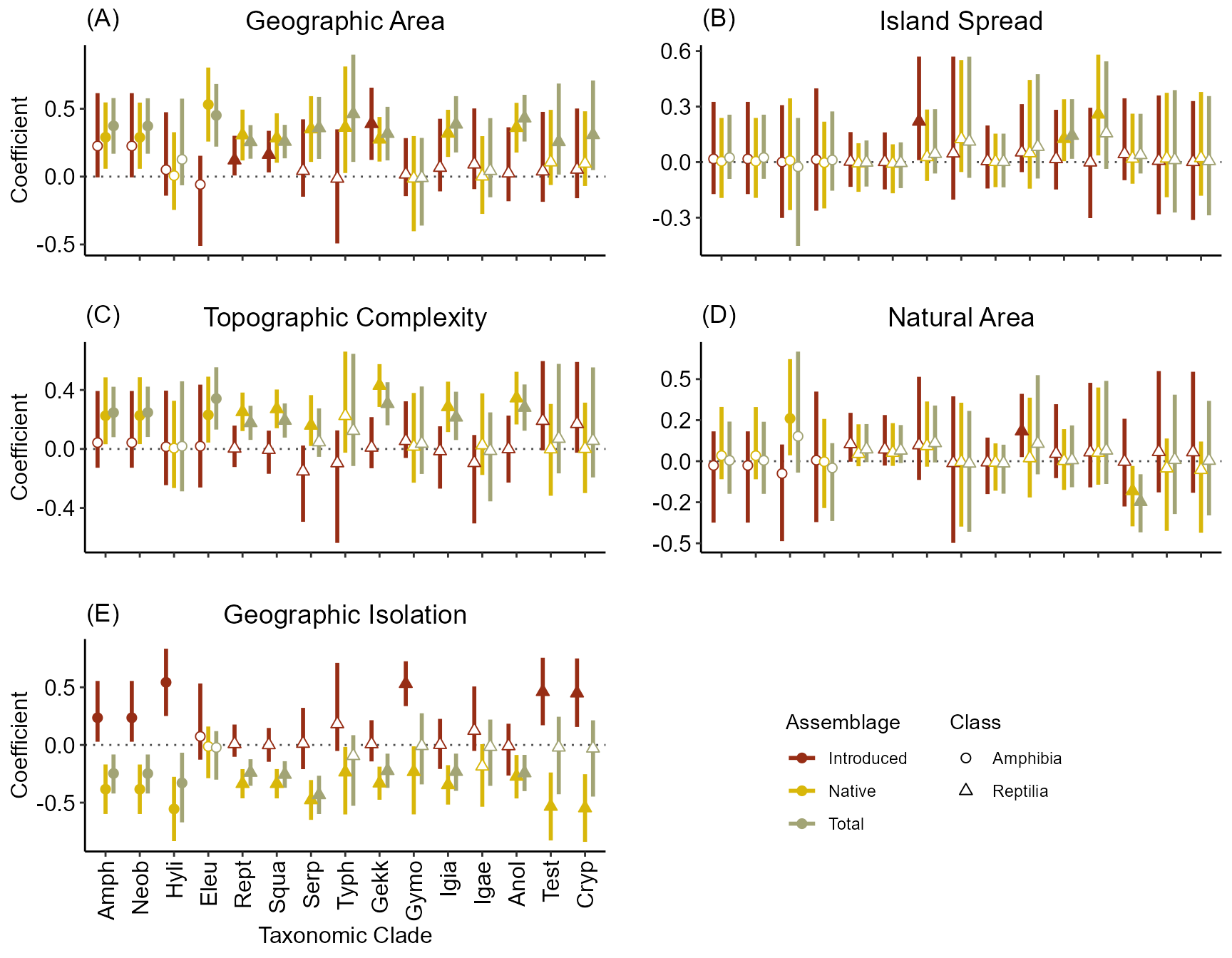

## TableGrob (3 x 2) "arrange": 6 grobs
##        z     cells    name           grob
## area   1 (1-1,1-1) arrange gtable[layout]
## spread 2 (1-1,2-2) arrange gtable[layout]
## topo   3 (2-2,1-1) arrange gtable[layout]
## green  4 (2-2,2-2) arrange gtable[layout]
## iso    5 (3-3,1-1) arrange gtable[layout]
## legend 6 (3-3,2-2) arrange gtable[layout]
ggsave(file.path(here(), 'data_out', 'results', 'sr_drivers', 'figs', 'Fig_5_psd-std.tif'), fig_4, 
       device = 'tiff', height = 7, width = 9, units = 'in', dpi = 300)

\(\space\)

\(\space\)

\(\underline{Anthropogenic \space Variables:}\) 

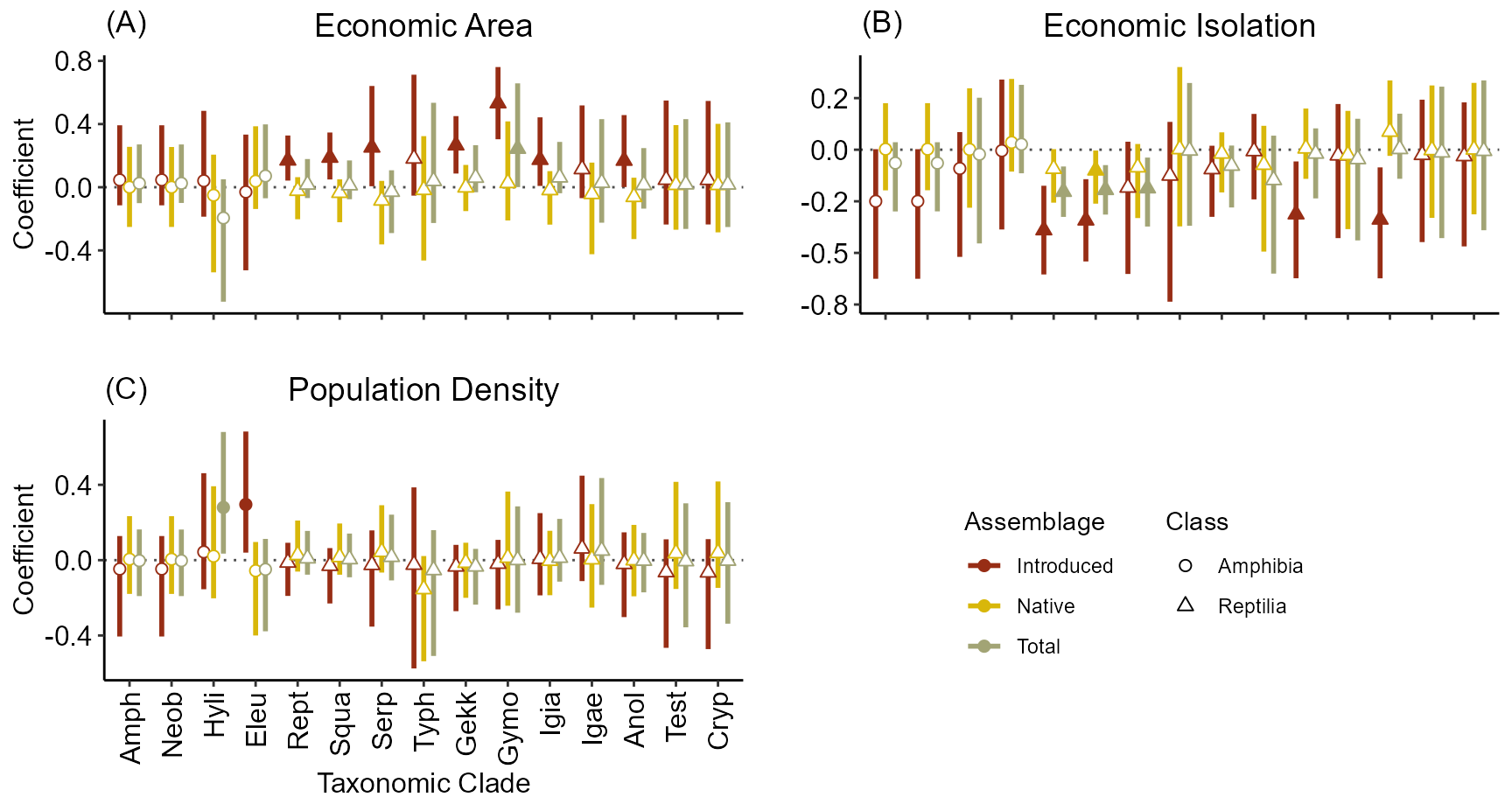
## TableGrob (2 x 2) "arrange": 4 grobs
##        z     cells    name           grob
## anthro 1 (1-1,1-1) arrange gtable[layout]
## ships  2 (1-1,2-2) arrange gtable[layout]
## pop    3 (2-2,1-1) arrange gtable[layout]
## legend 4 (2-2,2-2) arrange gtable[layout]
ggsave(file.path(here(), 'data_out', 'results', 'sr_drivers', 'figs', 'Fig_6_psd-std.tif'), fig_5, 
       device = 'tiff', height = 4.83, width = 9, units = 'in', dpi = 300)

We can also look at the largest reptile and amphibian genera in the Caribbean oth of which are of great interest to evolutionary and macroecologists.

\(\space\)

\(\underline{Anolis:}\)

\(\space\)

\(\space\)

\(\underline{Eleutherodactylus:}\)

We can see that overall the relationships are similar across taxonomic groups. However, some interesting differences are apparent.

First, for reptiles, higher DEM.sd (elevation variability) increases native SR, but all other relationships are similar to that of all herpetofauna. The importance of DEM.sd also comes out in the Amphibian. However, this may be due to its slightly high correlation with the bumber of ship visits since the amount of trade tends to increase exotic species propagule pressure. In addition, we can see that area becomes less important for SR as we move to smaller (and younger) taxonomic clades.

\(\space\)

\(\space\)

Average Model Fit

So far none of our analysis tells us whether or not our averaged models are actually good for describing the patterns of SR in the Caribbean. For that we need to calculate the R2 for the averaged model. This is done using the r_squared function in the ‘caribmacro’ package.

data <- lm.sr[['Data']]
vars2 <- attr(lm.sr[['Models']][[1]]$terms,'term.labels')

nams<-strsplit(names(data), ".", fixed = TRUE)
nams<-data.frame(matrix(unlist(nams), nrow = length(nams), byrow = TRUE))
names(nams) <- c('Taxon', 'Group')
nams$Taxon <- as.character(nams$Taxon)
nams$Group <- as.character(nams$Group)

R.sq_sr <- data.frame(NULL)
system.time(for (i in 1:length(data)) {
  temp <- Avg.SR[which(Avg.SR$Taxon == nams[i, 'Taxon'] &
                       Avg.SR$Group == nams[i, 'Group']), c('Variable', 'Estimate')]

  if (any(!is.na(temp$Estimate))) {

    tmp <- r_squared(temp,
                     data = data[[i]],
                     response = names(data)[i],
                     x_vars = vars2,
                     display = FALSE)
  } else {
    tmp <- data.frame(R.sq = NA,
                      adj.R.sq = NA)
  }

  tmp <- cbind(nams[i, ], tmp)
  R.sq_sr <- rbind(R.sq_sr, tmp)
})
##    user  system elapsed 
##    0.58    0.00    0.58
write.csv(R.sq_sr, file.path(here(), 'data_out', 'SR_Drivers_R_sq.csv'), row.names=FALSE)

If we just look at the R2 values for the groups we explored before, we can see that the SR models fit very nicely with exception of Exotic Eleutherodactylus community. However, the PSV models do not fit as well and only the PSV models for large clades or the the models with zeros consistantly had R2 values above 0.33 but not nearly as high as the SR models.

R Squared Values

\(\space\)

\(\underline{Herpetofauna:}\)

tmp <- R.sq_sr[which(R.sq_sr$Taxon == 'All'), ]

tmp$Sig <- ' '
tmp[which(tmp$R.sq > 0.33), 'Sig'] <- '*'
tmp[which(tmp$adj.R.sq > 0.33), 'Sig'] <- '*'
tmp[which(tmp$R.sq > 0.33 & tmp$adj.R.sq > 0.33), 'Sig'] <- '**'
tmp <- tmp[order(tmp$Group), c("Taxon", "Group", "R.sq", "adj.R.sq", "Sig")]

tab <- flextable(tmp)
tab <- colformat_double(tab, digits = 3)
tab <- align(tab, align = "center")
tab <- align(tab, j = 1:2, align = "right")
tab <- align(tab, j = 3:4, align = "left")
tab <- color(tab, i = 1, j = 5, color = "grey90", part = "header")
tab <- bold(tab, i = ~ Sig == '**')
tab <- width(tab, j = 'Sig', width = 0.1)
tab <- bg(tab, bg = 'grey90', part = 'all')
theme_vanilla(tab)

\(\space\)

\(\space\)

\(\underline{Reptilia:}\)

\(\space\)

\(\space\)

\(\underline{Amphibia:}\)

\(\space\)

\(\space\)

\(\underline{Anolis:}\)

\(\space\)

\(\space\)

\(\underline{Eleutherodactylus:}\)

\(\space\)

\(\space\)

## Warning: Removed 2 rows containing missing values (`geom_bar()`).
## Removed 2 rows containing missing values (`geom_bar()`).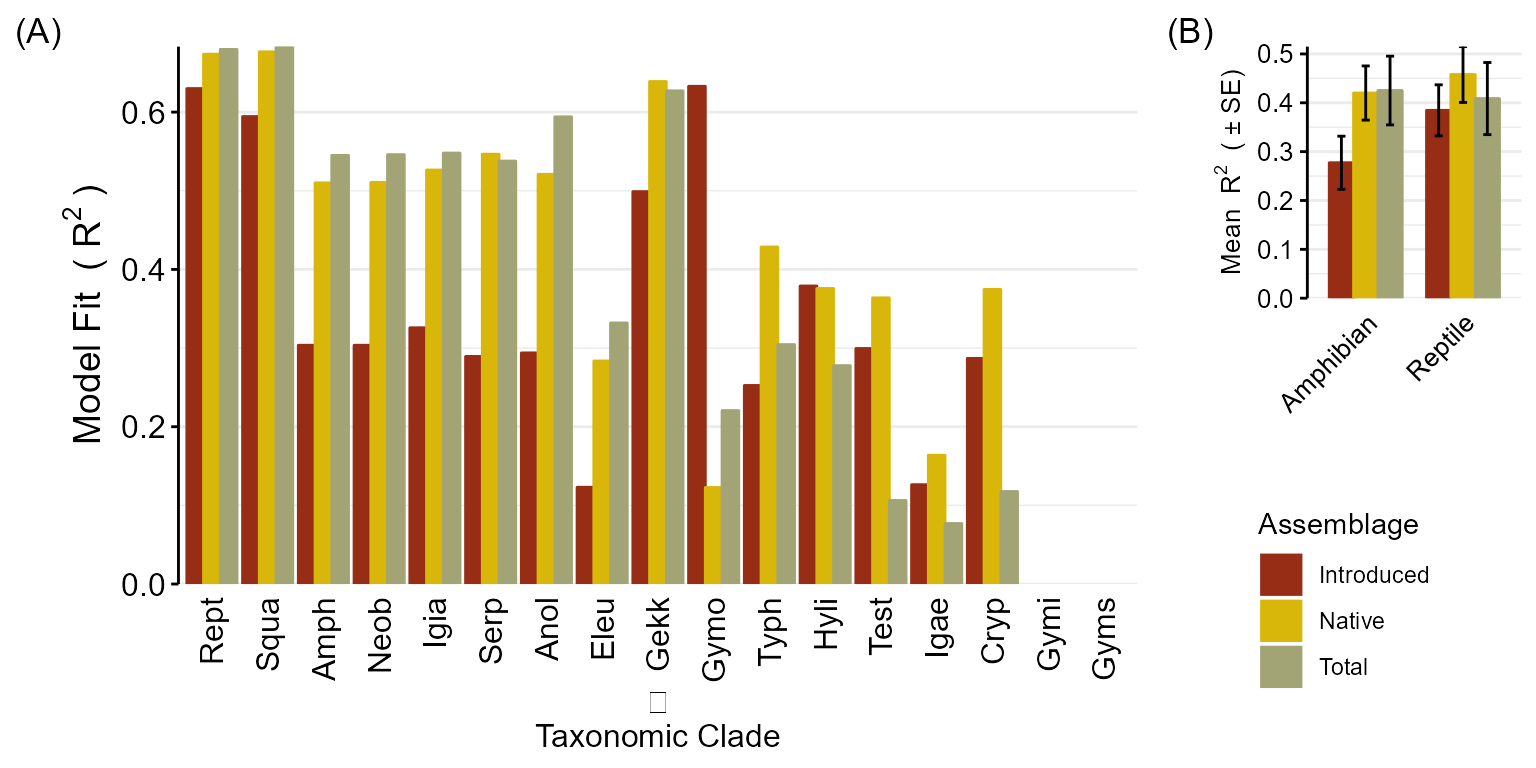

## TableGrob (4 x 2) "arrange": 3 grobs
##   z     cells    name           grob
## 1 1 (1-4,1-1) arrange gtable[layout]
## 2 2 (1-2,2-2) arrange gtable[layout]
## 3 3 (3-4,2-2) arrange gtable[layout]
\[\underline{END}\]

  1. Temple University, ↩︎